Query: in analysis, what does l2 refer to as a set?
Quick Answer:
The set L2 refers to the space of square-integrable functions. Specifically[1]:
On a measure space , the set of square integrable L2-functions is an -space. Taken together with the L2-inner product with respect to a measure , the -space forms a Hilbert space. The functions in an -space satisfy. The inequality ( 7) is called Schwarz's inequality . The basic example is when with Lebesgue measure.
In other words, L2 is the set of functions defined on a measure space whose square is Lebesgue integrable. It forms an inner product space called a Hilbert space when equipped with the L2 inner product.
Notice how many words appear to be missing from these sentences. I believe that this is because the source is https://mathworld.wolfram.com/L2-Space.html, in which most “text” is actually SVGs rendered from LaTeX, which Kagi doesn't know how to parse. So whereas we see
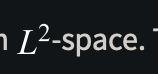
Kagi just sees “[[svg]]-space”.
I don't know what the general solution to this problem is, but Kagi should at least be cognizant of when images are interleaved with text and carry semantic information. In this case, the SVGs have alt-text, so Kagi should pull from there instead of just skipping over the images. (The screen capped L^2’s alt text is, in fact, “L^2”.)